Introduction
This article reviews the techniques to mitigate noise and vibrations due to magnetic forces in electrical machines (electromagnetically-excited noise and vibrations) based on EOMYS Engineering consulting experience. To go further, some online or in-person technical trainings are regularly organized for engineers involved in the development of electrical systems.
Noise and vibration control techniques of e-motors can be classified in three types:
- reduction of the structural response independently of the electromagnetic excitations
- reduction of the electromagnetic excitations independently of the structural response
- reduction of the number of resonances occuring between electromagnetic excitations and structural modes

The most efficient acoustic noise mitigation techniques are based on the cancellation of the harmonic electromagnetic excitations responsible for vibration and noise.
All these noise control techniques can be applied at early electromagnetic design stage using Manatee software for the fast calculation of noise and vibrations in electric motors.
Choice of the topology
There is no unique choice for a low noise & vibration machine, but some topologies are more challenging in terms of NVH. This also depends on the application constraints (e.g. power density, fixed speed or variable speed application).
Outer rotor topologies (also called outrunner motor if it is a brushless DC motor) can lead to higher noise & vibration due to rotor yoke lower stiffness compared to an outer stator topology. Fractional-slot winding or more particularly concentrated or tooth winding might lead to higher acoustic noise & vibrations compared to integral distributed winding due a higher number of wavenumbers in the armature field and the possible presence of subharmonics.
The best armature winding is the one creating the most sinusoidal mmf, so the double-layer, shorted-pitch, distributed integral winding. For permament magnet rotors, the best magnet architecture is also the one creating the most sinusoidal rotor mmf, so either Hallbach configuration for surface magnets, or multi-barriers V-shape interior magnets with bread-loaf pole shapes (also called sinusoidal field poles).
Manatee software can be used to calculate the NVH behaviour of all types of radial flux electric machines, including interior (buried), inset and surface permanent magnet synchronous machines, squirrel cage induction machines, outer rotor and inner rotor electrical machines.
New topologies can be easily implemented upon request.

Machine SPMSM_015 Topology
Asymmetries
An electric machine designed to have low harmonic distortion rate magnetomotive forces (e.g. an IPMSM with double-layer shorted-pitch distributed-winding, and V-shaped magnets) can reveal noisy due to manufacturing & assembly tolerances which introduce asymmetries.
Static and dynamic eccentricities increase the spectral density (wavenumbers & frequencies) of harmonic magnetic forces.
Mass & stiffness asymetries (and low number of teeth, introducing discrete distribution of stiffness along yoke) increase the modal density and number of resonances at variable speed.
Uneven airgap modulates magnetic forces and increases the number of different force wavenumbers, increasing the number of structural resonances.

Effect of asymmetries on electromagnetically-excited noise using Manatee V1 software (left: no asymmetry, right: with asymmetries)
To lower noise and vibrations the machine should be magnetically and geometrically symmetrical:
- low tolerance on eccentricities and misalignments
- low tolerance on lamination roundness
- low tolerance on magnet magnetization dispersion
- low tolerance on magnet position in slots
Manatee software can consider the NVH effect of 3D static and dynamic eccentricities, as well as uneven airgap.
Choice of the pole / slot / phase numbers
Generalities
Increasing the number of slot per pole per phase reduces the harmonic density of airgap flux and resulting magnetic forces.
Increasing the number of pole pairs gives a lower electromagnetic yoke height, thus higher vibration & noise. However, the lowest force wavenumber is also given by the Greatest Common Divider between stator slot and pole numbers in Permanent Magnet Synchronous Machines: increasing p also potentially increases GCD(Zs,2p), resulting in lower electromagnetic vibrations.
These examples show that changing the slot/pole/phase combination involves different electromagnetic and vibro-acoustic opposite effects, so numerical simulation with Manatee software is advised.
Case of induction machines
The number of rotor slots Zr is a key design parameter as it influences both wavenumbers and frequencies of Maxwell harmonic forces. Pole/slot interactions in induction machines create exciting forces at multiples of the rotor slot passing frequency.
Some empirical rules to choose the slot / pole combination are given in many electrical engineering books such as [1-5]. However these rules are continuous, they do not reflect correctly the discrete nature of harmonic force wave and do not account for the stator natural frequencies nor the speed range of the machine. The use of such empirical rules should be avoided and numerical simulation is advised for instance with Manatee software.

Effect of the rotor bar number on the maximum sound level emitted by a variable-speed induction motor (MANATEE software output)
When both stator slot and rotor slot numbers Zs & Zr are even integers, Maxwell force harmonics only contain even force wavenumbers for integral windings, thus avoiding Unbalance Magnetic Pull.
The number of rotor and stator slots should never be equal, otherwise strong pulsating radial and tangential force waves appear in the machine, creating high air-borne noise the stator breathing mode and potentially high structure-borne noise due to torque ripple.
Contrary to Permanent Magnet Synchronous Machines where some global rules on slot / pole combination can be relevant, the case of induction machines is more complex. Ideally one should avoid the presence of high magnitude (due to first rank of permeance), “low” wavenumber so in particular one should avoid
- [Zr-Zs|=0, 2 or 4
- |Zr-Zs-2p|=0, 2 or 4
- |Zr-Zs+2p|=0, 2 or 4
Relying only these rules of thumbs for the design of an electric machine is suboptimal and risky. Again variable speed calculation of electromagnetically-excited noise is advised using Manatee software.
Case of synchronous machines
When stator slot is an even integers, Maxwell force harmonics only contain even force wavenumbers for integral windings, thus avoiding Unbalance Magnetic Pull. More precisely UMP only exists if |Zs-2p|=1.
Maximization of LCM(Zs,2p) increases the frequency of open-circuit pulsating (wavenumber r=0) radial and tangential force harmonics (in particular cogging torque and average radial force).
Minimization of GCD(Zs,2p) reduces the magnitude of open-circuit pulsating (wavenumber r=0) radial and tangential force harmonics (in particular cogging torque and average radial force).
Maximization of GCD(Zs,2p) increases the non-zero wavenumbers of open-circuit (and probably also partial load) magnetic forces, thus potentially reducing noise and vibration levels.
Simiarly to induction machines, one should avoid the presence of high magnitude (due to first rank of permeance), “low” wavenumber so in particular one should avoid
- [2p-Zs|=0, 2
The 12s10p PMSM machine is known to be prone to high vibration and noise because |2p-Zs|=2: in open-circuit and under commutation, many force harmonics have a wavenumber 2 and can resonate with the stator elliptical mode.
As you can see some of these rules of thumb are contradictory and changing the slot number also changes the magnitude of permeance harmonics, so full NVH variable speed simulation is recommended with Manatee software.
Choice of the winding
The ideal winding gives a sinusoidal mmf, it has an infinite number of phases ( no « belt harmonics »), an infinite number of slots (no « slot harmonics » or preferably no « step harmonics ») or no slot at all (“airgap winding”).
To avoid Unbalanced Magnetic Pull the winding-induced mmf should never have two harmonics separated of 1.
Concentrated winding / tooth-winding / fractional winding have the largest mmf distortion factor, however if properly designed they do not generate noise & vibrations.
Shorted-pitch distributed windings gives the smoothest magnetomotive force.
Short-pitching or chording technique consists in having several winding layers and shifting the winding pattern in each layer. The chording cannot reduce the largest mmf step harmonics at Zs-p and Zs+p space harmonics.
The coil pitch Y (in slots, between 0 and Zs/(2p)-1) can be chosen as (5/6) Zs/(2p) to reduce the stator mmf space harmonics 5p and 7p.
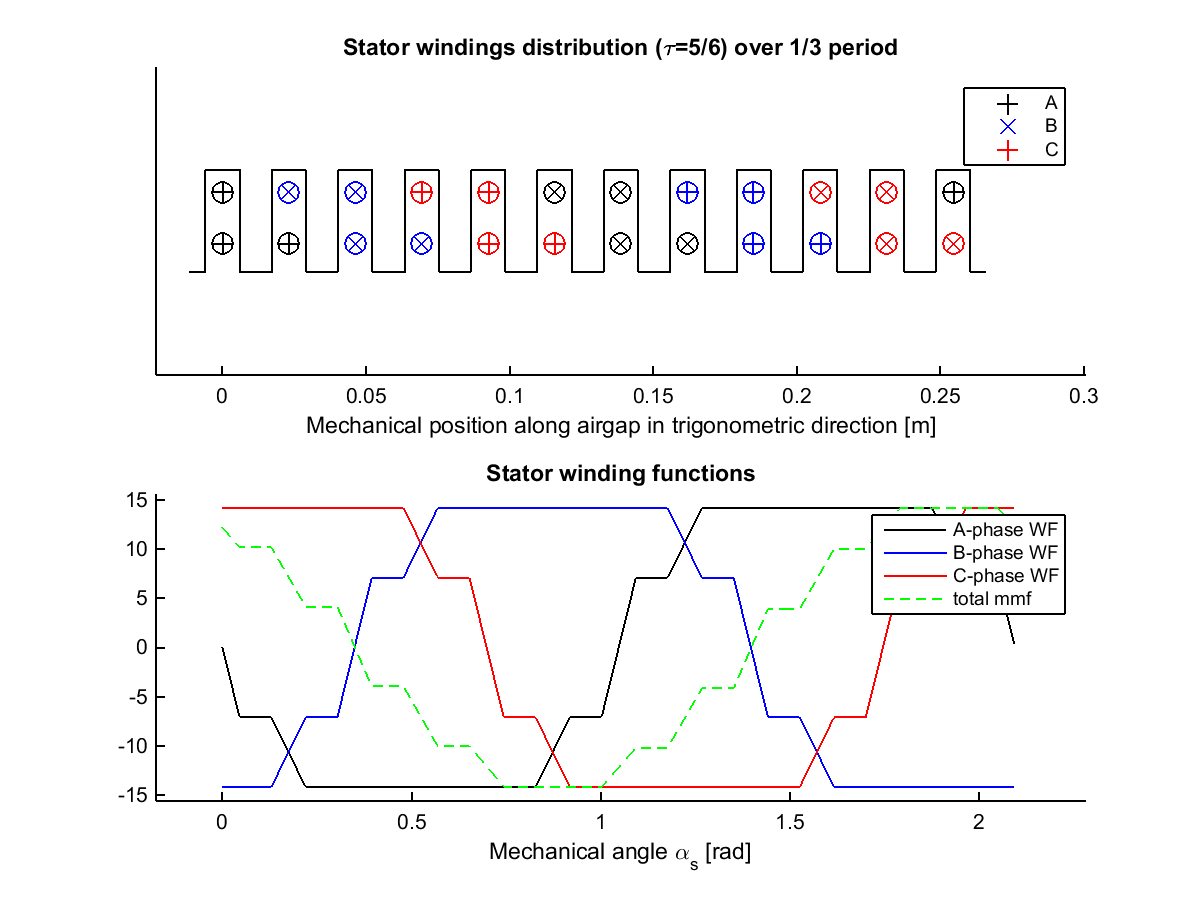
Example of an AC winding distribution (MANATEE V1 output)
All winding types can be modelled in Manatee software.
Skewing
Skewing consists in rotating a 2D slice of the electrical machine along its rotation axis in order to smoothen the average field and cancel out some specific harmonics. Skewing can be applied to stator, rotor or both.
Stator skew is generally linear, and rotor skew depends on machine topology (linear for squirrel cages, stepped-skew or linear for permanent magnets).
Skewing can cancel a given force harmonics when considering its average longitudinal value (DC component). However, it also introduces an axial magnetic force variation and can therefore excite longitudinal structural modes of the stator and rotor structures. It can also create an additional axial thrust.
The skewing angle and the part to be skewed (rotor or stator) depends on the magnetic force harmonic to be cancelled.
The best skewing angle might be different when trying to minimize torque harmonics or radial force harmonics, and the best skewing angle might depend on the load condition.
This task can be carried using Manatee simulation environment where any type of skew shape can be modelled.

FEMM submodel to calculate a rotor notch effect
Pole magnetization
Playing on the magnetization pattern allows to tune the rotor mmf harmonic content and thereof influence the vibroacoustic behaviour of the electric motor.
Hallbach pattern lowers the spatial harmonic content of mmf but is expensive to manufacture.
Shaping the magnetization pattern and optimizing the pole dimensions to minimize some specifics harmonics involved in noise generation is not sufficient to obtain a low vibration and noise design, as some other harmonics may increase during this process, creating new resonances.
A full electromagnetic and NVH simulation is recommended with Manatee software.
Pole shaping
Magnet / pole shoe shaping allows to « tune » the rotor mmf harmonic content and thereof the vibroacoustic behaviour of the electric machine.
As both constructive and destructive interference occurs, cancelling a given magnet mmf space harmonic responsible for acoustic noise does not necessarily reduce noise as it can increase other force harmonics.
For wound rotor synchronous machines the pole arc curvature has large influence on noise.
Due to the combined effect of radial and tangential forces on radial vibrations and noise, simulation with Manatee emotor design software is recommended.
Pole width and position
The pole widths or pole positions (pole shifting technique) of a synchronous machine can also be modulated to tune the rotor magnetimotive force spectrum content. Other pole displacement techniques to reduce cogging torque and zero-th average radial force include axial and radial pole-pairing technique (association of two different pole shapes to cancel a given harmonic).
Pole displacement techniques should be applied very carefully and should not focus only on the minimization of torque ripple / cogging torque, as noise and vibrations are also produced by higher wavenumber tangential and radial force harmonics. Simulation with Manatee virtual prototyping software is recommended.
Slot and tooth shape / position
Stator slot shapes or positions can be modulated to spread the permeance spatial spectrum or reduce / cancel a specific harmonic involved in noise and vibration generation.
Slot-pairing (teeth pairing) techniques can reduce cogging and average radial forces by cancelling the first component only at LCM(Zs,2p)fR.
Notches
Notches (sometimes called circumferential slits, auxiliary slots, dummy slots, or grooves) consists in removing some part of the magnetic sheet material to modulate the airgap reluctance.
If properly sized, notching can artificially increase the slot number was increased.
The average airgap is increased due to notches (increase of Carter coefficient) so it may slightly reduce the electromagnetic performances.
The introduction of notches can also increase the local saturation level.
Similarly to skewing, the e-NVH effect of notches strongly depends on considered operating point.
Simulation with Manatee software is recommended along max torque speed curve or even on full torque speed plane.
<media815|legende|titre|center|taille=moyen>
Stator slot opening optimization
The permeance harmonics are due to reluctance variation along the airgap, and slotting effects are a source of permeance harmonics at multiples of slot number.
Slot to tooth opening ratio can reduce some of the permeance harmonics (similarly to pole pitch to pole arc ratio for the rotor mmf), but it is influenced by saturation and sometimes several slotting harmonics are involved in noise generation
If the first stator slot harmonic (ks=1) is responsible for a force wave in a machine – ex: PMSM with Zs=12 and p=5, an airgap Maxwell stress harmonic force exists with waveumber r=(1*Zs-1*p)-(0+1*p)=2 – closing the slot theoretically cancel this particular stress harmonic.
In practice, closing the slots may not be possible due to winding process, or because magnetic saturation naturally enlarges the slot opening.
Optimal slot design can be carried using Manatee software for the prediction of electromagnetic noise and vibraitons.
Magnetic wedges
Magnetic wedges allow to reduce the magnetic reluctance change in the slot opening, reducing flux density slotting harmonics and therefore cogging torque and all magnetic force harmonics related to permeance harmonics.
Due to low relative permeability of commercial wedges (max 10) the effect on noise is limited (max 3 dB).
The impact of magnetic wedges on e-motor vibroacoustics can be studied within Manatee e-NVH software.
Airgap increase
Airgap increase can affect differently magnetic force harmonics, so noise may even increase when increasing airgap. Besides, changing the airgap strongly changes the electromagnetic performances so when working at constant torque or constant efficiency, one must include the change of control when studying the impact of airgap change.
The effect of airgap width can be studied within Manatee software parameter sweep environment.
Flux barriers
Flux barriers or pockets in stator yoke and teeth, or rotor yoke and teeth can modify the airgap flux harmonic content and magnetic force magnitude due to local saturation effects.
It generally significantly affects the machine performances (increase of leakage inductance, reduction of torque) so it must be used carefully.

Effects of flux barrier dimensions on the harmonic content of airgap flux obtained with MANATEE software
Manatee software can be used to size the flux barriers during emachine development.
Control
Case of induction machines
Magnetic noise is linked to magnetizing flux and not to torque, it is possible to increase torque with constant flux and noise.
Manatee software simulation allows to find the trade-offs between vibroacoustic and electrical performances.
Case of synchronous machines
Current angle or load angle has a strong influence on average magnetic force magnitude.
The load angle can influence the magnitude of higher time harmonics of wavenumber r=0 tangential & radial forces. The load angle evolution of force harmonics depends on their frequency and wavenumber. Iq changes both pulsating r=0 radial and tangential force harmonics (torque), while Id mainly changes pulsating radial force harmonics. Field weakening (negative Id ) may reduce pulsating radial force ripple while increasing tangential force ripple.
A detailed sensitivity analysis including structure-borne and air-borne noise under Manatee software is advised to study the tradeoffs between optimal control for efficiency (e.g. MTPA) and optimal control for noise reduction.
Harmonic current injection
Generalities
A given vibration harmonic can be compensated by injecting additional harmonic currents, depending on the magnetic force wavenumber to be cancelled.
As the current modulates the spatial harmonics of mmf winding functions, the current injection cannot create new wavenumbers than those already present in the magnetic forces. Current injection introduces new time harmonics and therefore new force harmonics (cf PWM lines), one must check that this does not worsen the vibration or noise level nor torque ripple.
High frequency noise is more difficult to damp with current injection (e.g. requires higher controller bandwith). Harmonic injection at 6f in DQH frame can damp r=0 pulsating harmonic force at 6f.
Synchronous machines
For synchronous machines, pulsating radial / tangential force waves magnitude at frequencies proportional to LCM(Zs,2p)fs/p can be damped using current injection. For radial force damping either Id or Iq harmonic injection theoretically works.
Induction machines
Radial force harmonics of wavenumbers 0 and 2p can be damped using current injection. For other wavenumbers, a detailed study must be carried.
Manatee software includes a special e-NVH mitigation environment to optimize harmonic current injection with respect to acoustic noise and torque ripple.
Switching strategies
Generalities
Voltage inverter switching strategies determine phase voltage harmonic content and resulting phase current spectrum. Supply voltage harmonics contain harmonics linked to the inverter Pulse Width Modulation (PWM) switching frequency (ex: fswi, 2fswi) and harmonics linked to fundamental (ex: 5f, 7f). The largest voltage, current, forces, vibration and noise harmonics can occur around once or twice the switching frequency depending on the PWM strategy and torque/speed operating point of the machine.
A voltage harmonic f creates a harmonic current f which in turn generates magnetic forces and vibration waves f+fs, 2p and f-fs, 0 where fs is the fundamental electrical frequency.
Increasing the switching frequency generally reduces the acoustic noise (dBA reduction above 2.5 kHz), in some cases it can be chosen out from human’s ear sensitivity. However, it significantly increases inverter losses so again tradeoffs between efficiency and NVH must be analyzed, which can be carried under Manatee software.
Spread spectrum strategies
Spread spectrum principle is already used in aerodynamic noise (uneven blade spacing of fans). The same principle is used in randomized switching strategies.
Such strategies may lower the maximum dBA level, but they result in a wider excitation spectrum which can lead to new resonances depending on damping and natural frequency position with respect to exciting forces. Finally, random strategies can significantly affect sound perception and a detailed sound quality study is advised.
Manatee software includes some sound quality metrics to study this effect.
PWM strategies
There are many PWM strategies such as SPWM, SVPWM, DPWM0, DPWM1, DPWM2, DWPM3, DPWMmin, DPWMmax, GDPWM.
These commutations strategies have been developed to maximize converter output and efficiency, and they change the excitation voltage spectra and resulting sound power level as well as sound quality metrics.
All these PWM strategies are already implemented in Manatee e-NVH software, which also includes sound quality metrics to optimize power electronics switching strategy.
Structural response
Lower noise & vibration can be achieved by putting natural frequencies further away from magnetic excitations.
Stator yoke can be stiffened to reduce vibration and noise levels ; in this case one must check that the natural frequency change due to the yoke geometry change does not compensate noise and vibration reduction due to yoke stiffening.
Manatee software can be used to automatically study the effect of lamination shape on acoustic noise.
Other techniques to play on both air-borne and structure-borne noise include
- optimize yoke geometry
- optimize coupling between lamination and housing
- optimize slot stiffness (winding material, spacers)
- optimize stator fixation method in casing
Manatee software coupled to FEA can be used to optimize these couplings and find a way to reduce the overall noise levels considering all transfer paths.
Damping
Increasing damping is one of the most efficient techniques to reduce noise and vibration of electric machines. It includes:
- optimization of impregnation process (VPI, potting, dipping): materials, curing process, operating temperature
- use of higher damping magnetic sheets
- use of interlamination damping
- use of viscoelastic materials
References
[1] J.F. Gieras, C. Wang and J.C. Lai, Noise of polyphase electric motors, CRC Press, 2005.
[2] P.L. Timar, Noise and vibration of electrical machines, Elsevier, 1989.
[3] S.J. Yang, Low noise electrical motors, Clarendon Press, Oxford, 1981.
[4] PYRHONEN Juha, Tapani Jokinen, Valéria Hrabovcova, Design of Rotating Electrical Machines (2nd Ed.), Wiley, 2013
